Dibujar la frontera eficiente de dos activos

Si tenemos una inversión repartida entre varios activos, es decir, diversificada, nos gustaría saber cuál es la asignación óptima de cada activo de forma que maximicemos la rentabilidad sin aumentar el riesgo. Sobre esta cuestión trata buena parte de la literatura financiera desde que en 1952 Markowitz publicó su famoso artículo "Porfolio Selection" donde desarrolla el modelo media-varianza.

Si para simplificar, consideramos solo dos activos: A y B, la rentabilidad de nuestra cartera P será:

$$ r_P = w_A\cdot r_A + w_B\cdot r_B $$

, donde $ r_i$ son los vectores de rentabilidades cada activo y $ w_i$ son las ponderaciones. Debe cumplirse que: $ w_A + w_B = 1 $

Podemos simular las rentabilidades de distintas carteras combinando asignaciones diferentes entre A y B y representar gráficamente la media y la desviación típica (volatilidad) de la rentabilidad de cada una de estas carteras para obtenerla bala de Markowitz. Se observa que para cada nivel de riesgo hay dos carteras distintas y se espera que un inversor racional elija aquella cuya rentabilidad es superior, de aqui el concepto de cartera eficiente. La parte superior de la bala representa la frontera eficiente.

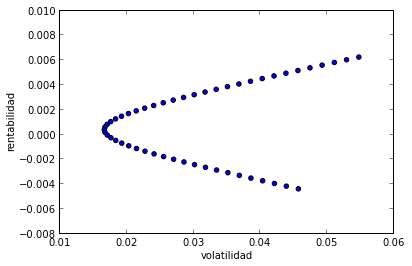
Se puede generalizar para n activos y la conclusión es la misma. En otro articulo veremos como encontrar la cartera óptima, donde en algunos casos nos ayudaran los multiplicadores de Lagrange y en otros tendremos que apoyarnos en métodos de optimización heurística. Y el código Python...

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas.io.data import DataReader
import datetime as dt

# Descarga datos de ejemplo
A = DataReader('TRE.MC', 'yahoo',
start = dt.datetime(2011, 1, 1),
end = dt.datetime(2011, 12 ,31))
B = DataReader('BME.MC', 'yahoo',
start = dt.datetime(2011, 1, 1),
end = dt.datetime(2011, 12, 31))

# Calcula la rentabilidad diaria de cada activo
A['ret'] = A['Adj Close'].pct_change()
B['ret'] = B['Adj Close'].pct_change()

# Simula las ponderaciones de 50 carteras
W = np.zeros([50, 2])
W[:,0] = np.linspace(-2, 2, 50)
W[:,1] = 1 - W[:,0]
W = pd.DataFrame(W, columns=['A','B'])

# Simula las rentabilidades de las distinas carteras
# y calcula la media y desviación tiípica de cada
# una de ellas.
P = np.zeros([50, 2])
for n in range(50):
pf = W.A[n] * A.ret.dropna() + W.B[n] * B.ret.dropna()
P[n] = pf.mean(), pf.std()

# Dibuja el gráfico
plt.scatter(P[:,1], P[:,0])
plt.xlabel('volatilidad')
plt.ylabel('rentabilidad')
plt.show()